Set Identities:
1 – Commutativity
Changing the order of elements won’t affect the results.
Example in Arithmetics: 5 + 4 = 4 + 5 = 9 and 3 x 1 = 1 x 3 = 3
The addition and multiplication of elements are commutative. Subtraction and division are not commutative.
A – Set union is commutative:
A \cup\,B\;=\;B\,\cup\,A\\this\;is\;like:\\A+B=B+A
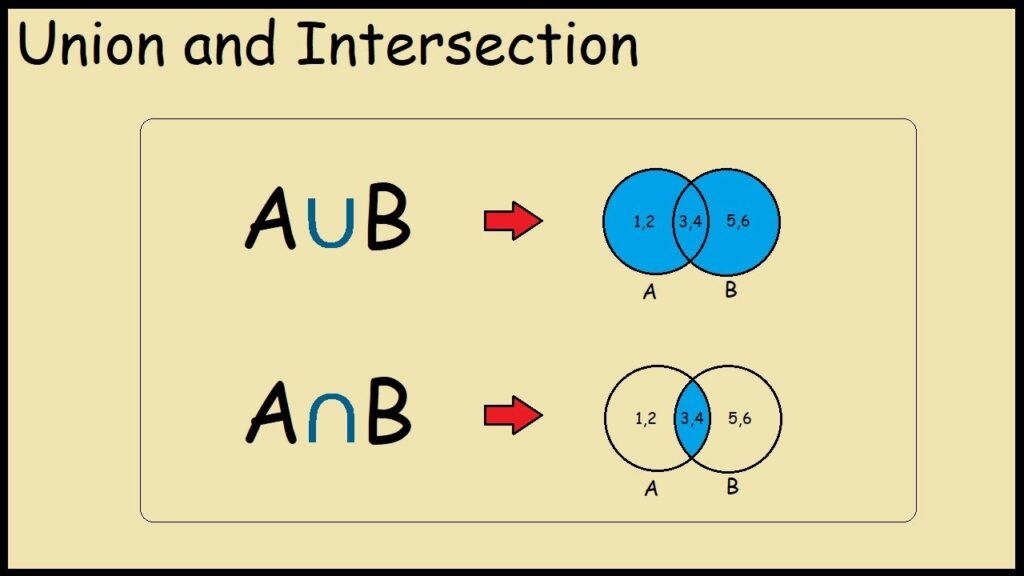
B – Set intersection is commutative:
A \cap\,B\;=\;B\,\cap\,A
Review: The intersection of two sets A and B, denoted by A∩B, consists of all elements that are both in A and B. For example, {1,2}∩{2,3}={2}.
C – Symmetric difference is commutative:
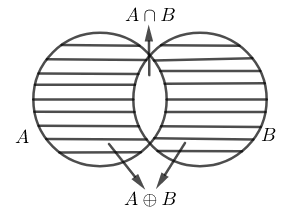
A\oplus B=B\oplus A
Review: The set which contains the elements which are either in set A or in set B but not in both is called the symmetric difference between two given sets.
Note that in some, the symbol Δ is used.
C – Set difference is NOT commutative.
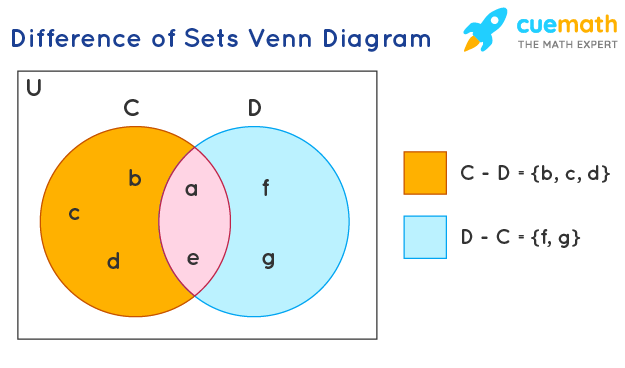
A-B\neq B-A
2 – Associativity
The associative property states that the sum or product of a set of numbers is the same, no matter how the numbers are grouped. An operation is associative if a change in grouping does not change the results. This means the parenthesis (or brackets) can be moved. Numbers that are added can be grouped in any order.
Example in Arithmetic:
(1 + 5)(6+1) = (1+1)(5+6) = 13
(3 * 5)(4 * 2) = (3 * 4)(5 * 2) = 120
The addition of numbers is associative.
A – Set union is associative:
(A\cup B)\cup C = A \cup (B\cup C)\\\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16\}=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16\}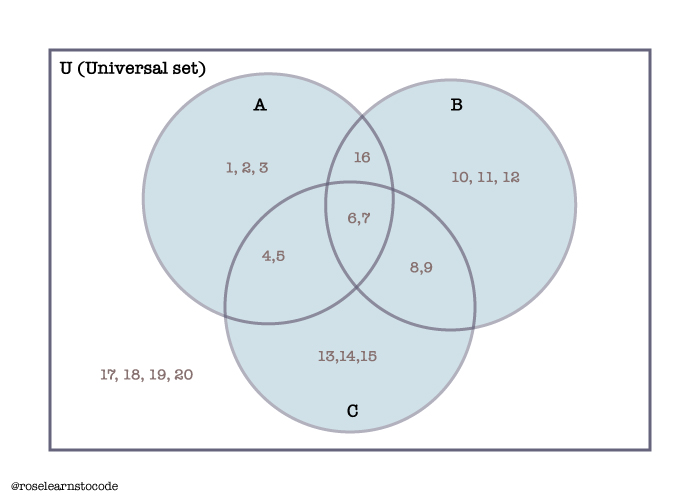
B – Set intersection is associative:
(A\cap B)\cap C=A\cap (B \cap C)\\(A\cap B)\cap C=A\cap (B \cap C)=A\cap B \cap C\\=\{4,5,6,7,8,9,16\}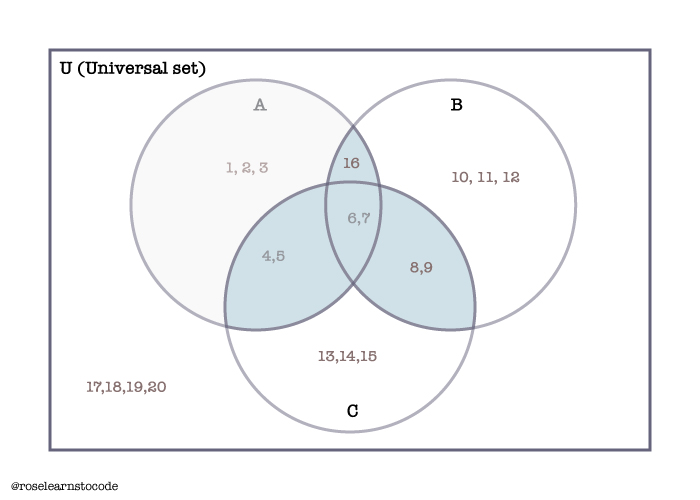
Reference:
- https://math.libretexts.org/Bookshelves/Applied_Mathematics/Contemporary_Mathematics_%28OpenStax%29/01%3A__Sets/1.06%3A_Set_Operations_with_Three_Sets
- https://www.cimt.org.uk/projects/mepres/book7/bk7i1/bk7_1i4.htm
A'=\overline{A}=complement\;of\;A=not\;AC – Symmetric difference is associative:
Again, symmetric difference are elements that are either in sets, but not in both. (elements in the intersection are not included)
(A\oplus B) \oplus C=A \oplus (B \oplus C)\\=A \oplus B \oplus C\\=\{1,2,3,10,11,12,13,14,15\}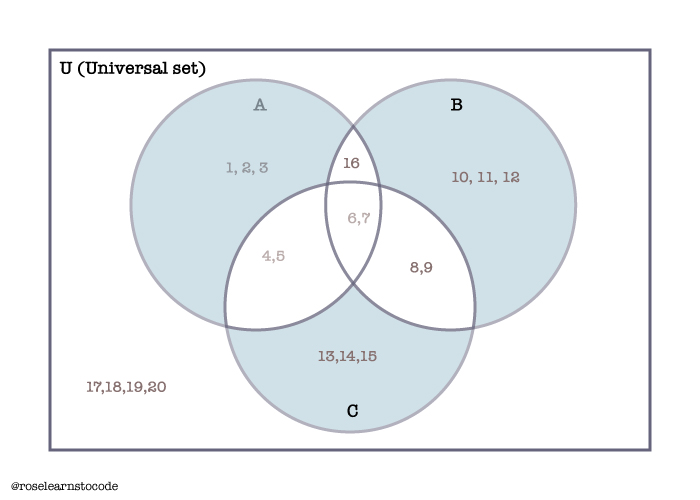
D- Set difference is NOT associative
Example:
A = {1,2,3,4,5,6,7,16}
B = {6,7,8,9,10,11,12,16}
C = {4,5,6,7,8,9,13,14,15}
(A-B)-C\\A=\{1,2,3,4,5,\cancel{6},\cancel{7}\cancel{16}\}\\B=\{\cancel{6},\cancel{7},8,9,10,11,12,\cancel{16}\}\\(A-B)=\{1,2,3,\cancel4,\cancel5\}\\(A-B)-C=\{1,2,3\}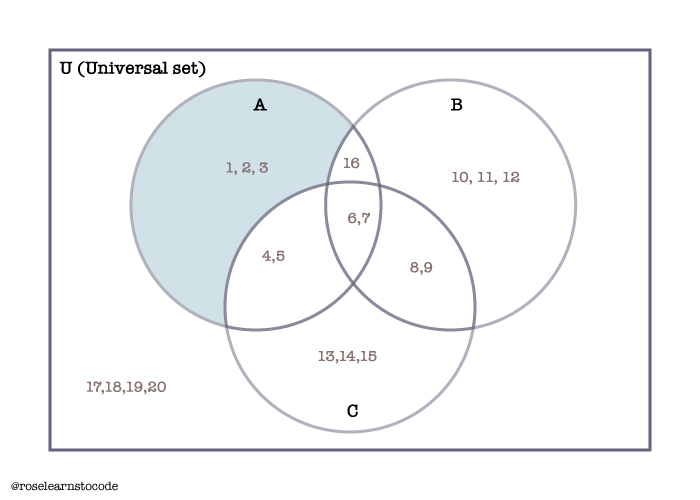
A-(B-C)\\B=\{\cancel6,\cancel7,\cancel8,\cancel9,10,11,12,16\}\\C=\{4,5,\cancel6,\cancel7,\cancel8,\cancel9,13,14,15\}\\B-C=\{10,11,12,\cancel{16}\}\\A=\{1,2,3,4,5,6,7,\cancel{16}\}\\A-(B-C)=\{1,2,3,4,5,6,7\}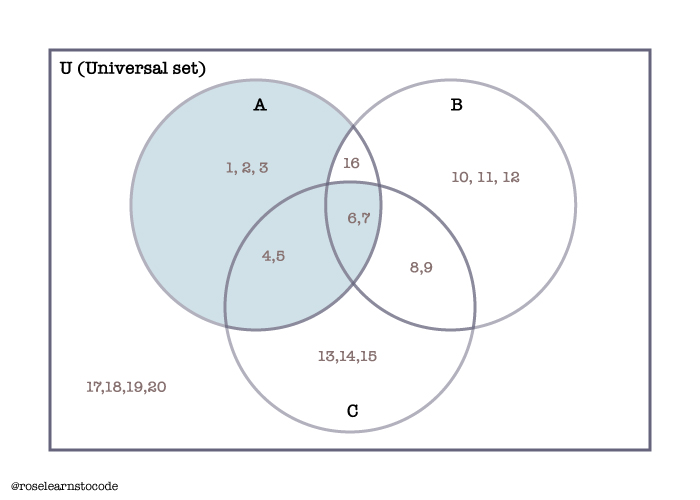
3 – Distributivity
Distributive Law states that, the sum and product remain the same value even when the order of the elements is altered.
The distributive property is sometimes called the distributive law of multiplication and division.
For example:
3*(2+5)=3*2+3*5=21
Given 3 numbers a, b, and c:
a(b+c)=ab+ac
We say that the multiplication is distributive over the addition.
A – The set union is distributive over the set of intersection:
A\cup(B\cap C)=(A\cup B)\cap(A \cup C)
B – The set intersection is distributive over the set of union:
A\cap(B\cup C)=(A \cap B) \cup (A \cap C)
Proof by membership tables 1
Note to self:
\cup = union = in\,logic,\,this\,is\,like\,or\,\vee\\\cap=intersection=in\,logic,\,this\,is\,like\,and\,\wedge
| A | B | C | B∩C | A∪(B∩C) | A∪B | A∪C | (A∪B)∩(A∪C) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Set Identities
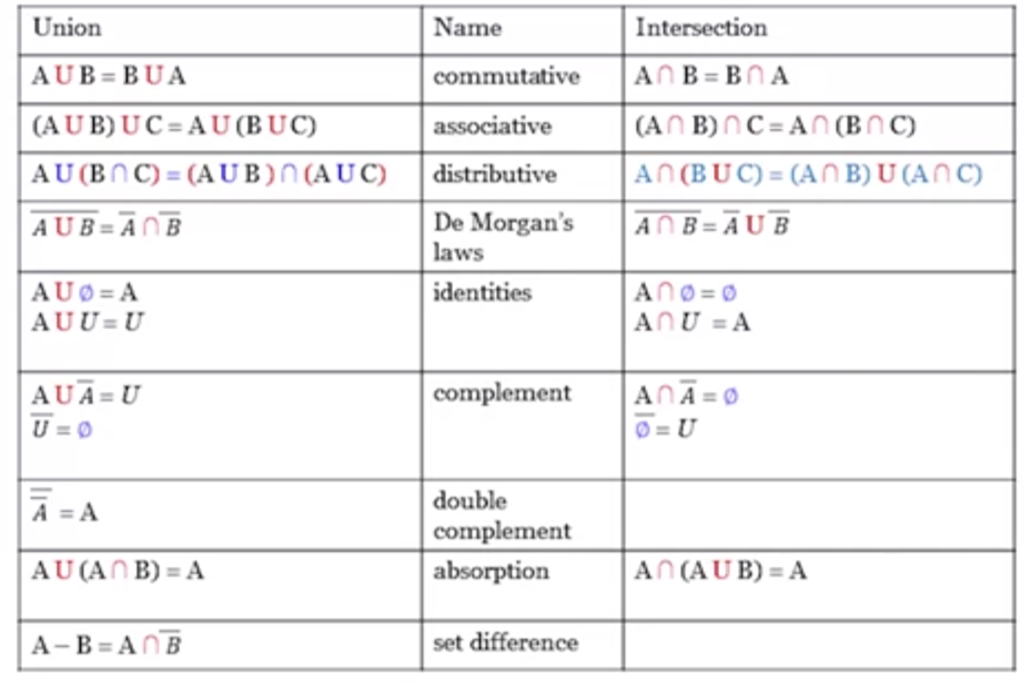
LaTex
- union = U = \cup
- intersection =
∩= \cap - symmetric difference = ⊕ = \oplus
Leave a Reply