De Morgan’s laws describe how mathematical statements and concepts are related through their opposites. In set theory, De Morgan’s laws relate to the intersection and union of sets through their complements.
The structure of De Morgan’s laws, whether applied to sets, propositions or logic gates, is always the same.
First Law
The complement of the union of two sets A and B is equal to the intersection of their complements.
\overline{A\cup B}\;=\;\overline{A}\;\cap\;\overline{B}Second Law
The complement of the intersection of two sets A and B is equal to the union of their complements.
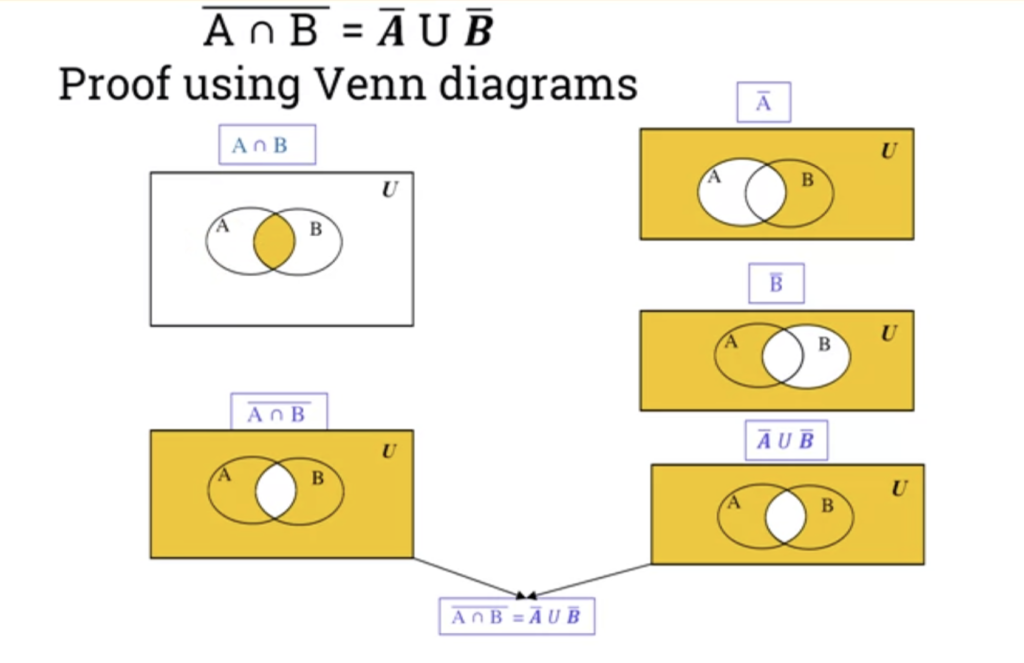
\overline{A\cap B}\;=\;\overline{A}\;\cup\;\overline{B}Proof Using Membership Table
\overline{A\cup B}\;=\;\overline{A}\;\cap\;\overline{B}

Proof using Venn Diagrams

Notes from Quiz:
\overline{A}\;\cap\;B\;=\;\overline{A\cup \overline{B}}To review for next lesson: Laws of Sets:
Leave a Reply